Pi

Dans les dictionnaires et ouvrages généralistes, π est défini comme le rapport, constant dans le plan usuel qu’est le plan euclidien, entre la circonférence d’un cercle et son diamètre.

Ce rapport ne dépend pas du cercle choisi, en particulier de sa taille.
En effet, tous les cercles sont semblables et pour passer d’un cercle à un autre il suffit de connaître le rapport de la similitude.

Par suite, pour tout réel positif k, si un cercle possède un rayon r (ou un diamètre d = 2r) k fois plus grand qu’un autre, alors son périmètre P sera aussi k fois plus grand, ce qui prouve la constance du rapport.

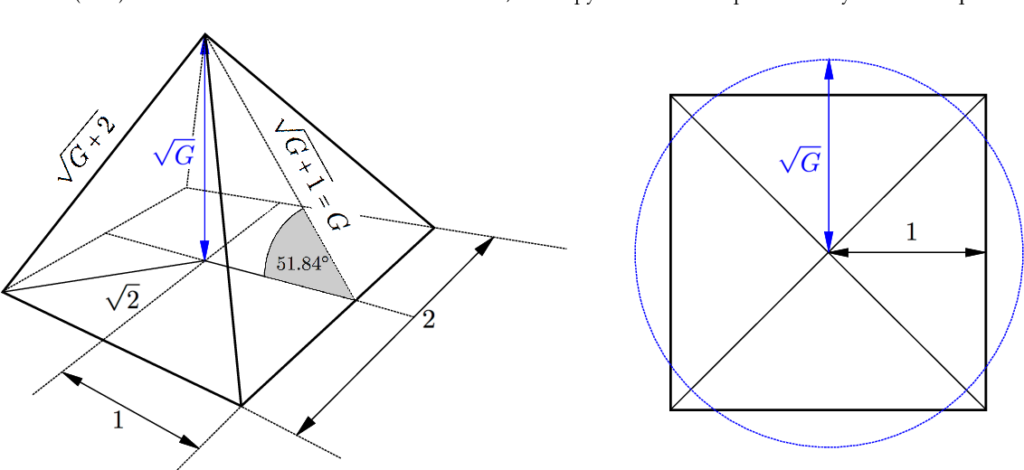
Il est naturel (à la lumière de ces deux exemples) de se demander comment on peut trouver de telles approximations. Est-ce simplement en cherchant plus ou moins au hasard ou bien y-a-t-il un moyen plus systématique d’y parvenir ?

La pyramide de Khéops a été scrutée et mesurée avec autant de précision que possible par des chercheurs issus de différents domaines depuis le début du xix^e siècle.
De ces mesures ont découlé plusieurs hypothèses sur la volonté de ses concepteurs d’utiliser quelques éléments mathématiques dans ses proportions.

Afin de comparer les différents résultats et d’analyser les intentions des concepteurs, les mesures sont exprimées en coudées égyptiennes.
La pyramide avait ainsi, à l’origine, une base de 440 coudées et une hauteur de 280 coudées. La pente de ses faces est alors donnée par le rapport 280/220 soit 14/11.
Ce rapport, étant un nombre sans dimension, reste bien entendu le même quelle que soit l’unité de mesure considérée.

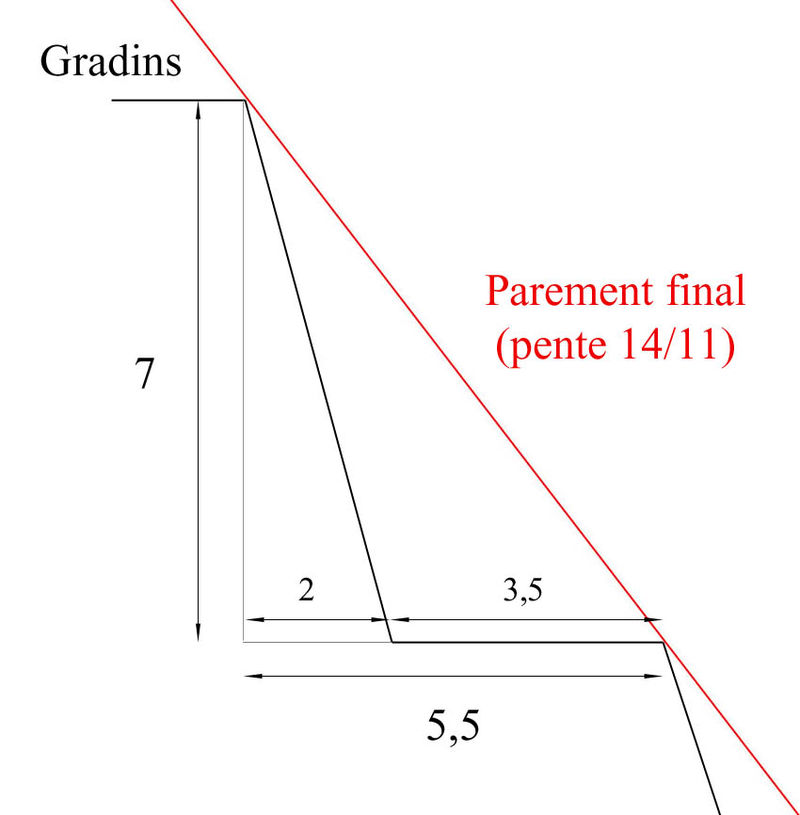
Quand on étudie la géométrie de la grande pyramide, il est délicat de faire la distinction entre les intentions des constructeurs et les propriétés qui découlent des proportions de l’édifice.
On mentionne souvent le nombre d’or φ et le nombre Pi présents dans les proportions de la pyramide : les Égyptiens ont, nous l’avons vu, choisi une pente pour les faces de 14/11.